Der Robbins-Monro-Prozess ist ein stochastischer Prozess, mit dessen Hilfe die Nullstelle einer unbekannten Regressionsfunktion stochastisch approximiert werden kann. Er wurde 1951 von Herbert Robbins und Sutton Monro vorgestellt.
Definition
Sei  eine Familie von Zufallsvariablen und
eine Familie von Zufallsvariablen und  eine messbare Funktion, sodass gilt:
eine messbare Funktion, sodass gilt:  . Sei zudem eine eindeutige Lösung
. Sei zudem eine eindeutige Lösung  gegeben, sodass
gegeben, sodass  .
Dann heißt die Folge
.
Dann heißt die Folge  von Zufallsvariablen gegeben durch
von Zufallsvariablen gegeben durch

Robbins-Monro-Prozess, wobei  eine beliebige reelle Konstante und
eine beliebige reelle Konstante und  eine Folge reeller Konstanten mit
eine Folge reeller Konstanten mit  sei.
sei.
Konvergenz von Xn gegen θ
Unter den folgenden vier Bedingungen konvergiert  in
in  gegen
gegen  [1]:
[1]:
![{\displaystyle \exists {C>0}\forall {x\in \mathbb {R} }\ (P[\left|Y_{x}\right|\leq C]=1)}](./edb60423496cac8f2317e73d918dbabab61478a1.svg) ,
, ist monoton wachsend,
ist monoton wachsend, existiert,
existiert, genügt folgenden Bedingungen:
genügt folgenden Bedingungen:

Einfaches Beispiel
Seien  um
um  verschobene Sinusfunktionen zwischen
verschobene Sinusfunktionen zwischen  und
und  mit zufälligen Schwankungen
mit zufälligen Schwankungen  , die an den Rändern linear fortgesetzt werden.
, die an den Rändern linear fortgesetzt werden.

Wobei  unabhängige, gleichverteilte Zufallsvariablen in
unabhängige, gleichverteilte Zufallsvariablen in  sind.
Sei außerdem
sind.
Sei außerdem  und
und  . Dann konvergiert
. Dann konvergiert  gegen
gegen  .
.
-
Schaubild mit 5 verschiedenen Pfaden und 300 Iterationen. Die gestrichelte Linie bezeichnet dabei den Grenzwert

.
Einzelnachweise
- ↑ Herbert Robbins, Sutton Monro: A Stochastic Approximation Method. In: The Annals of Mathematical Statistics. 22, Nr. 3, 1951, S. 405 Theorem 2.
Literatur
- Herbert Robbins, Sutton Monro: A Stochastic Approximation Method. In: The Annals of Mathematical Statistics. 22, Nr. 3, 1951, S. 400–407(PDF-Datei; 514KB).
- Marie Duflo: Random Iterative Models, Springer Verlag, 1997.
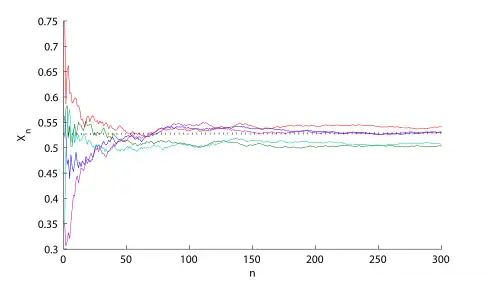 Schaubild mit 5 verschiedenen Pfaden und 300 Iterationen. Die gestrichelte Linie bezeichnet dabei den Grenzwert .
Schaubild mit 5 verschiedenen Pfaden und 300 Iterationen. Die gestrichelte Linie bezeichnet dabei den Grenzwert .