Hyperbolisches Dreieck

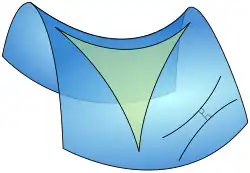
Ein hyperbolisches Dreieck ist in der hyperbolischen Geometrie ein Dreieck in der hyperbolischen Ebene. Es besteht aus drei Liniensegmenten, den Seiten oder Kanten, und drei Punkten, den Winkeln oder Scheitelpunkten. Wie bei einem Dreieck in der euklidischen Ebene liegen drei Punkte eines hyperbolischen Raums beliebiger Dimension immer auf derselben Ebene. Daher beschreiben planare hyperbolische Dreiecke auch Dreiecke, die in jeder höheren Dimension hyperbolischer Räume möglich sind.

Jedes hyperbolische Dreieck hat einen Inkreis, aber nicht jedes hyperbolische Dreieck hat einen Umkreis. Seine Eckpunkte können auf einem Horozykel oder Hyperzykel liegen.

Hyperbolische Dreiecke haben einige Eigenschaften, die denen von Dreiecken in der sphärischen oder elliptischen Geometrie ähneln:

• Zwei Dreiecke mit gleicher Winkelsumme haben den gleichen Flächeninhalt.
• Es gibt eine Obergrenze für den Flächeninhalt von Dreiecken.
• Es gibt eine Obergrenze für den Radius des Inkreises.
• Zwei Dreiecke sind genau dann kongruent, wenn sie unter einem endlichen Produkt von Linienspiegelungen korrespondieren.
• Zwei Dreiecke mit gleichen zugehörigen Winkeln sind kongruent, d. h. alle ähnlichen Dreiecke sind kongruent.

Hyperbolische Dreiecke haben einige Eigenschaften, die den Eigenschaften von Dreiecken in der sphärischen oder elliptischen Geometrie entgegengesetzt sind:

• Die Winkelsumme eines Dreiecks ist kleiner als 180°.
• Die Fläche eines Dreiecks ist proportional zum Defizit seiner Winkelsumme von 180°.

Hyperbolische Dreiecke haben außerdem einige Eigenschaften, die in anderen Geometrien nicht vorkommen:

• Manche hyperbolische Dreiecke haben keinen Umkreis. Dies ist der Fall, wenn mindestens einer ihrer Scheitelpunkte ein idealer Punkt ist oder wenn alle Scheitelpunkte auf einem Horozykel oder einem einseitigen Hyperzykel liegen.
• Hyperbolische Dreiecke sind dünn, d. h. es gibt einen maximalen Abstand ${\displaystyle \delta }$ von einem Punkt auf einer Kante zu einer der beiden anderen Kanten. Dieses Prinzip führte zum ${\displaystyle \delta }$-hyperbolischen Raum.

Die Definition eines Dreiecks lässt sich verallgemeinern, indem Eckpunkte auf dem idealen Rand der Ebene liegen, die Seiten jedoch innerhalb der Ebene verbleiben. Ist ein Seitenpaar Grenzparallelität (d. h. der Abstand zwischen ihnen nähert sich Null, wenn sie zum Idealpunkt tendieren, sich aber nicht schneiden), so enden sie an einem idealen Eckpunkt, der als Omegapunkt dargestellt wird. Man kann auch sagen, dass ein solches Seitenpaar einen Nullwinkel bildet. Ein Dreieck mit einem Nullwinkel ist in der euklidischen Geometrie für gerade Seiten, die auf unterschiedlichen Linien liegen, unmöglich. Bei Tangentialkreisen sind solche Nullwinkel jedoch möglich. Ein Dreieck mit einem idealen Eckpunkt wird als Omegadreieck bezeichnet.

Die Beziehungen zwischen Winkeln und Seiten sind analog zu denen der sphärischen Trigonometrie. Die Längenskala sowohl für die sphärische Geometrie als auch für die hyperbolische Geometrie kann beispielsweise als die Länge einer Seite eines gleichseitigen Dreiecks mit festen Winkeln definiert werden. Die Längenskala ist am praktischsten, wenn die Längen in absoluten Längen gemessen werden (eine spezielle Längeneinheit analog zu den Beziehungen zwischen Entfernungen in der sphärischen Geometrie). Diese Wahl dieser Längenskala vereinfacht die Formeln.

Im Poincaré-Halbebenenmodell entspricht die absolute Länge der infinitesimalen Metrik ${\displaystyle ds={\frac {|dz|}{\operatorname {Im} (z)}}}$ und im Poincaré-Scheibenmodell ${\displaystyle ds={\frac {2|dz|}{1-|z|^{2}}}}$.

Bezüglich der (konstanten und negativen) gaußschen Krümmung einer hyperbolischen Ebene entspricht eine absolute Längeneinheit einer Länge von ${\displaystyle R={\frac {1}{\sqrt {-K}}}}$.

In einem hyperbolischen Dreieck ist die Summe der Innenwinkel ${\displaystyle A}$, ${\displaystyle B}$ und ${\displaystyle C}$ (jeweils gegenüber der Seite mit dem entsprechenden Buchstaben) kleiner als ein gestreckter Winkel. Die Differenz zwischen dem Maß eines gestreckten Winkels und der Summe der Winkelmaße eines Dreiecks wird als Defekt des Dreiecks bezeichnet. Die Fläche eines hyperbolischen Dreiecks ist gleich seinem Defekt multipliziert mit dem Quadrat von ${\displaystyle (\pi -A-B-C)R^{2}{}{}\!}$. Dieser Satz, der erstmals von Johann Heinrich Lambert bewiesen wurde, ist mit dem Satz von Girard in der sphärischen Geometrie verwandt.

Für jedes hyperbolische Dreieck mit den Seitenlängen ${\displaystyle a}$, ${\displaystyle b}$, ${\displaystyle c}$ und den Innenwinkeln ${\displaystyle A}$, ${\displaystyle B}$, ${\displaystyle C}$ gilt der hyperbolische Kosinussatz:

${\displaystyle \cosh(c)=\cosh(a)\cdot \cosh(b)-\sinh(a)\cdot \sinh(b)\cdot \cos(C)}$

Sein dualer Satz lautet:

${\displaystyle \cos(C)=-\cos(A)\cdot \cos(B)+\sin(A)\cdot \sin(B)\cdot \cosh(c)}$

Es gilt außerdem folgende Formel:

${\displaystyle \cos(C)\cdot \cosh(a)=\sinh(a)\cdot \coth(b)-\sin(C)\cdot \cot(B)}$

Es gibt auch einen Sinussatz für hyperbolische Dreiecke:

${\displaystyle {\frac {\sin(A)}{\sinh(a)}}={\frac {\sin(B)}{\sinh(b)}}={\frac {\sin(C)}{\sinh(c)}}}$

Für jedes rechtwinklige hyperbolische Dreieck mit dem rechten Winkel ${\displaystyle C}$ gilt:

Der Sinus des Winkels ${\displaystyle A}$ ist der hyperbolische Sinus der dem Winkel gegenüberliegenden Seite geteilt durch den hyperbolischen Sinus der Hypotenuse.

${\displaystyle \sin(A)={\frac {\sinh(a)}{\sinh(c)}}}$

Der Kosinus des Winkels ${\displaystyle A}$ ist der hyperbolische Tangens der angrenzenden Kathete geteilt durch den hyperbolischen Tangens der Hypotenuse.

${\displaystyle \cos(A)={\frac {\tanh(b)}{\tanh(c)}}}$

Der Tangens des Winkels ${\displaystyle A}$ ist der hyperbolische Tangens der gegenüberliegenden Kathete geteilt durch den hyperbolischen Sinus der benachbarten Kathete.

${\displaystyle \tan(A)={\frac {\tanh(a)}{\sinh(b)}}}$

Der hyperbolische Kosinus der Ankathete des Winkels ${\displaystyle A}$ ist der Kosinus des Winkels ${\displaystyle B}$ geteilt durch den Sinus des Winkels ${\displaystyle A}$.

${\displaystyle \cosh(b)={\frac {\cos(B)}{\sin(A)}}}$

Der hyperbolische Kosinus der Hypotenuse ist das Produkt des hyperbolischen Kosinus der Katheten.

${\displaystyle \cosh(c)=\cosh(a)\cdot \cosh(b)}$

Der hyperbolische Kosinus der Hypotenuse ist auch das Produkt der Kosinuswerte der Winkel geteilt durch das Produkt ihrer Sinuswerte.

${\displaystyle \cosh(c)={\frac {\cos(A)\cdot \cos(B)}{\sin(A)\cdot \sin(B)}}=\cot(A)\cdot \cot(B)}$

Außerdem gelten folgende Gleichungen:^[1]

${\displaystyle \cos(A)=\cosh(a)\cdot \sin(B)}$

${\displaystyle \sin(A)={\frac {\cos(B)}{\cosh(b)}}}$

${\displaystyle \tan(A)={\frac {\cot(B)}{\cosh(c)}}}$

${\displaystyle \cos(B)=\cosh(b)\cdot \sin(A)}$

Aus den trigonometrischen Formeln für rechtwinklige hyperbolische Dreiecke lassen sich auch die Beziehungen zwischen der Seitenlänge ${\displaystyle s}$ und den Winkeln ${\displaystyle A}$ eines gleichseitigen hyperbolischen Dreiecks herleiten. Es gilt:^[1]

${\displaystyle \cos(A)={\frac {\tanh \left({\frac {s}{2}}\right)}{\tanh(s)}}}$

${\displaystyle \cosh \left({\frac {s}{2}}\right)={\frac {\cos \left({\frac {a}{2}}\right)}{\sin(A)}}={\frac {1}{2\cdot \sin \left({\frac {A}{2}}\right)}}}$

• Tristan Needham: Visual Complex Analysis. Clarendon Press, 1997, ISBN 978-0-19-853446-4 (google.de). 
• John Ratcliffe: Foundations of Hyperbolic Manifolds. Springer Science & Business Media, 2006, ISBN 978-0-387-33197-3 (google.de). 
• hyperbolic geometry. University of Glasgow, abgerufen am 28. August 2025. 

1. ↑ ^{a b} George E. Martin: The foundations of geometry and the non-Euclidean plane. Corrected 4. print. Auflage. Springer, New York, NY 1998, ISBN 0-387-90694-0, S. 433 (englisch, archive.org).