Eckfigur (Geometrie)

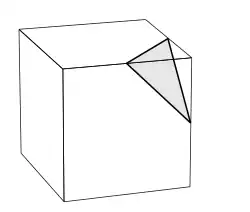
Eine Eckfigur ist eine geometrische Beschreibung der Umgebung einer Ecke eines ${\displaystyle d}$-dimensionalen Polytops oder einer ${\displaystyle d}$-dimensionalen Parkettierung. Die Ecken der Eckfigur sind durch die Mittelpunkte aller Kanten, die von einer Ecke ausgehen, definiert.^[1][2] Für ein ${\displaystyle d}$-dimensionales Polytop ist die Eckfigur daher ein Polytop der Dimension ${\displaystyle d-1}$. So ist beispielsweise die Eckfigur eines Polyeders ein Polygon. In der nebenstehenden Abbildung ist dargestellt, dass die Eckfigur eines Würfels ein gleichseitiges Dreieck ist.

Ein regelmäßiges Polytop oder eine regelmäßige Parkettierung lassen sich durch ein Schläfli-Symbol ${\displaystyle \left\{p,q,\ldots ,v,w\right\}}$ beschreiben.^[3] Bei einem regelmäßigen ${\displaystyle d}$-dimensionalen Polytop enthält das Schläfli-Symbol ${\displaystyle d-1}$ Zahlen. Bei der Parkettierung des ${\displaystyle d}$-dimensionalen Raums enthält es ${\displaystyle d}$ Zahlen. Beispielsweise stellt das Schläfli-Symbol ${\displaystyle \left\{4,3\right\}}$ einen dreidimensionalen Würfel dar und das Schläfli-Symbol ${\displaystyle \left\{4,3,4\right\}}$ die Parkettierung des dreidimensionalen Raums mit Würfeln.

Die Zellen, die das Polytop begrenzen, werden durch die ersten ${\displaystyle d-2}$ Zahlen ${\displaystyle \left\{p,q,\ldots ,v\right\}}$ des Schläfli-Symbols beschrieben. Für die Zellen, die bei einer ${\displaystyle d}$-dimensionalen Parkettierung den Raum ausfüllen, sind dies entsprechend die ersten ${\displaystyle d-1}$ Zahlen des Schläfli-Symbols.^[3] Beispielsweise sind die Flächen (die zweidimensionalen Zelle) des Würfels ${\displaystyle \left\{4,3\right\}}$ Quadrate ${\displaystyle \left\{4\right\}}$ und die Polyeder (die dreidimensionalen Zelle) der Parkettierung ${\displaystyle \left\{4,3,4\right\}}$ Würfel ${\displaystyle \left\{4,3\right\}}$.

Analog dazu wird die Eckfigur eines Polytops durch die letzten ${\displaystyle d-2}$ Zahlen ${\displaystyle \left\{q,\ldots ,v,w\right\}}$ des Schläfli-Symbols beschrieben. Bei der ${\displaystyle d}$-dimensionalen Parkettierung sind dies entsprechend die letzten ${\displaystyle d-1}$ Zahlen des Schläfli-Symbols.^[3] Beispielsweise sind die Eckfigur eines Würfels ${\displaystyle \left\{4,3\right\}}$ ein gleichseitiges Dreieck ${\displaystyle \left\{3\right\}}$ und die Eckfigur der Parkettierung ${\displaystyle \left\{4,3,4\right\}}$ des dreidimensionalen Raumes mit Würfeln ein regelmäßiges Oktaeder ${\displaystyle \left\{3,4\right\}}$.

Die Eckfigur eines regelmäßigen Polygons ${\displaystyle \left\{p\right\}}$ ist eine Strecke ${\displaystyle \left\{\right\}}$. Wenn das Polygon die Seitenlänge ${\displaystyle 2l}$ hat, ist die Länge der Strecke ${\displaystyle 2l\cos(\pi /p)}$.^[4] Diese Formel gilt auch für Sterne.^[5] Für diese ist ${\displaystyle p}$ eine rationale Zahl.

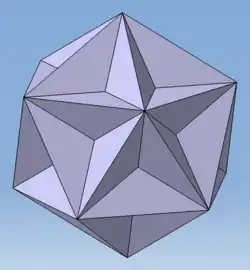
Platonische Körper, Kepler-Poinsot-Körper und Platonische Parkettierungen der Ebene werden durch ein Schläfli-Symbol ${\displaystyle \left\{p,q\right\}}$ beschrieben. Sie bestehen aus regelmäßigen p-Ecken ${\displaystyle \left\{p\right\}}$ und haben ein regelmäßiges q-Eck ${\displaystyle \left\{q\right\}}$ als Eckfigur. Beispielsweise besteht ein Ikosaeder ${\displaystyle \left\{3,5\right\}}$ aus gleichseitigen Dreiecken und hat ein regelmäßiges Fünfeck als Eckfigur, während ein großes Dodekaeder ${\textstyle \left\{5,{\frac {5}{2}}\right\}}$ aus regelmäßigen Fünfecken besteht und ein Pentagramm als Eckfigur hat.

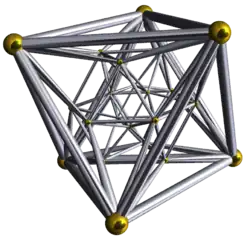
Es gibt 16 regelmäßige vierdimensionale Polytope – sechs konvexe und zehn sternförmige.^[6] Sie werden durch ein Schläfli-Symbol ${\displaystyle \left\{p,q,r\right\}}$ beschrieben, bestehen aus Platonischen Körpern oder Kepler-Poinsot-Körpern ${\displaystyle \left\{p,q\right\}}$ und haben die Eckfigur ${\displaystyle \left\{q,r\right\}}$. Beispielsweise besteht der Tesserakt ${\displaystyle \left\{4,3,3\right\}}$ aus Würfeln ${\displaystyle \left\{4,3\right\}}$; seine Eckfigur ist ein regelmäßiges Tetraeder ${\displaystyle \left\{3,3\right\}}$. Als weiteres Beispiel besteht das regelmäßige 24-Zell ${\displaystyle \left\{3,4,3\right\}}$ aus Oktaedern ${\displaystyle \left\{3,4\right\}}$ und hat Würfel ${\displaystyle \left\{4,3\right\}}$ als Eckfigur. Als abschließendes Beispiel besteht das Sternpolytop ${\textstyle \left\{5,{\frac {5}{2}},3\right\}}$ aus großen Dodekaedern ${\textstyle \left\{5,{\frac {5}{2}}\right\}}$ und hat Ikosaedersterne ${\textstyle \left\{{\frac {5}{2}},3\right\}}$ als Eckfigur. Die einzige regelmäßige Parkettierung ${\displaystyle \left\{4,3,4\right\}}$ des dreidimensionalen Raumes wurde schon oben beschrieben.

Aus einem Polytop kann ein neues Polytop durch ein symmetrisches Abschneiden einer Umgebung jeder seiner Ecken erzeugt werden. Der abzuschneidende Teil der Eckumgebung wird durch einen festen Abstand auf den von der Ecke ausgehenden Kanten festgelegt. Dieser Vorgang wird Abstumpfung genannt. Wenn bis zur Mitte der Kanten, also bis zur Eckfigur, abgestumpft wird, spricht man von Rektifikation. Beispielsweise können durch Rektifikation der platonischen Körper zwei archimedische Körper erzeugt werden: die Rektifikation des Würfels oder des Oktaeders erzeugt das Kuboktaeder, die des Ikosaeders oder Dodekaeders das Ikosidodekaeder.

Würfel	Kuboktaeder	Oktaeder
Rektifikation →		← Rektifikation

In der nebenstehenden Abbildung ist die Abstumpfung eines Würfels und eines Oktaeders zum Kuboktaeder dargestellt. Die Abbildung veranschaulicht außerdem, dass die Eckfigur eines Würfels ein gleichseitiges Dreieck und die eines Oktaeders ein Quadrat ist.

1. ↑ H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 16, 68, 128 (englisch). 
2. ↑ H. S. M. Coxeter: Unvergängliche Geometrie (= Wissenschaft und Kultur. Band 17). 2. Auflage. Birkhäuser, Basel 1981, ISBN 978-3-0348-5152-7, S. 58, 86, 196, 477, doi:10.1007/978-3-0348-5151-0 (englisch: Introduction to Geometry. New York 1969. Übersetzt von J. J. Burchhardt). 
3. ↑ ^{a b c} H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 128–129 (englisch). 
4. ↑ H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 16 (englisch). 
5. ↑ H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 94 (englisch). 
6. ↑ H. S. M. Coxeter: Regular Polytopes. 3. Auflage. Dover Publications, New York 1973, ISBN 0-486-61480-8, S. 292–295 (englisch).